Back to Electronics

Self-Learning: Phase Shift Oscillator

Oct. 2023 (ongoing)

In a world where just about everything has to have a microcontroller and internet connectivity, I've always thought there is a certain beauty in precisely-designed analog circuits. I recently had a free afternoon and decided to jump into learning about one such category of circuits I've seen in a few places: the humble analog sine wave oscillator.

Unlike the Pierce oscillator (used to generate the clock signal by most digital systems) and the beloved 555 timer, which both create square waves, the phase-shift oscillator is one of a handful of commonly-used sine wave oscillators.

Contents

Theory/Background

For a closed-loop system to maintain oscillation, it must meet a few requirements:

Phase-shift oscillator block diagram
Phase-shift oscillator block diagram

The theoretical phase-shift oscillator circuit is comprised of two main subsections:

  1. An (inverting) amplifier stage (α)
  2. A feedback path with a phase shift of 180° (β)

As I understand it, the basic operating principle of a phase-shift oscillator is as follows:

The amplifier can be considered to have a phase-shift of 180° due to its inverting configuration, as long as the input signal is periodic. The feedback path consists of reactive components which will together introduce a phase shift of 180° at a particular frequency. The phase shift of the amplifier normally won't change (much), so the reactivity of the feedback path will cause the oscillation frequency to adjust until the total phase shift of the loop reaches equilibrium at 360°.

Circuit Analysis

Deriving the Feedback Path

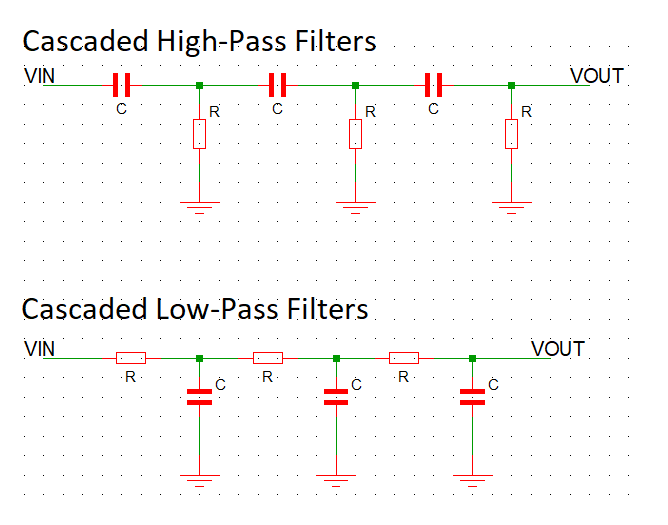
Phase-shift oscillator feedback schematics
Three-stage feedback path circuits

I figured the best place to start would be the feedback path because it will determine the frequency of oscillation.

The feedback path must provide 180° of phase shift at the desired frequency. Most phase-shift oscillator designs use three cascaded low-pass or high-pass RC filters. A single-stage RC filter can provide up-to 90° of phase shift, so at least two are required for the oscillator to function properly. Using a three-stage filter, each stage contributes around 60°, but not equally. This is because the impedance of each successive stage loads down the previous stage. The following calculations assume all three resistors are equal and all three capacitors are equal.

I used Kirchhoff's Current Law to find the transfer functions of these circuits (as it happens, both functions share the same form making it possible to find both at the same time by substituting the complex term that differs). I derived the transfer functions to be:

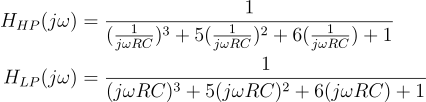
To determine the frequency of oscillation, we can use the transfer function to find the frequency at which the phase shift is 180°:

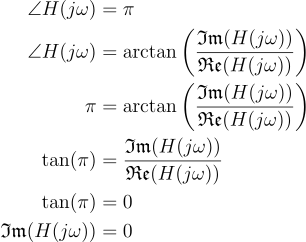
For the high-pass feedback path:

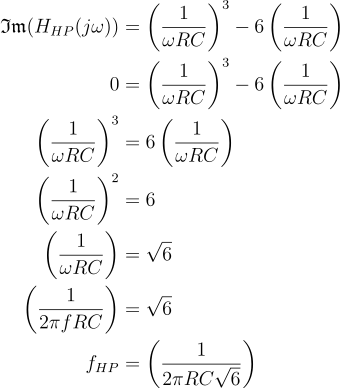
For the low-pass feedback path:

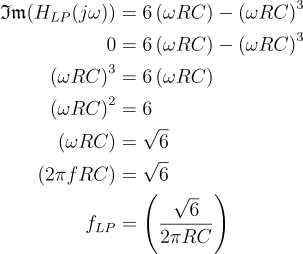
Next, we need to know what the gain of the feedback path will be at the oscillating frequency. It turns out this is independent of the resistor and capacitor values, and the result is the same no matter which topology you choose.

High pass:

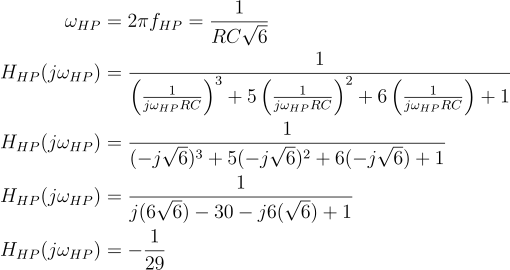
Low pass:

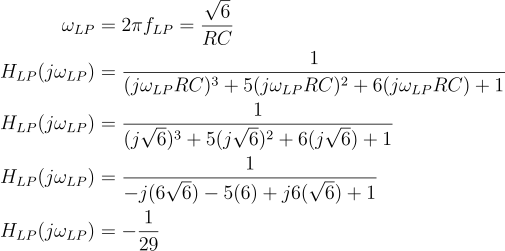
Finally, we can validate these formulas with real numbers. As an example, I used 10 kΩ resistors and 10 nF capacitors in a low-pass configuration. According to the above formulas,

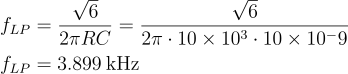
The gain in decibels is:

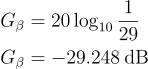
These values can be seen on the Bode plot of the feedback path:

I also plotted both low-pass and high-pass configurations together to highlight an observation: built with the same components, an oscillator using the low-pass feedback path will oscillate at a higher frequency than one built with the high-pass configuration. In the plot below, the blue lines represent the high-pass filter and the orange lines represent the low-pass filter.

In the phase plot, the oscillation frequency is where we see the jump from -π to +π (the phase crossover frequency).

The ratio of oscillation frequencies is constant:

Forward Path

Because the theoretical loop gain must equal 1, this means the amplifier in the forward path has to have a gain of -29 to compensate for the loss in the feedback path. The two most commonly-used components are an NPN bipolar transistor or an op-amp, but it is also possible to use a different amplifier such as a vacuum tube.

Designing a 1 kHz Oscillator

In my experience, the best way to learn something is to do it. I thought about it for a while and settled on some basic requirements to aim for.

Requirements

  1. Frequency: 1 kHz ± 5% (or 0.95 kHz to 1.05 kHz)
  2. Amplitude: fixed 12 V peak-to-peak ± 5% (or 11.4 V to 12.6 V)
    • Alternatively, an adjustable output amplitude is acceptable if a fixed amplitude cannot be reliably achieved.
  3. Power: must be able to operate on a ±12 V power supply (like this one)
  4. Assembly: should be easy to assemble with minimal tools and commonly-available components (through-hole construction, etc.)

Design Choices

In the design of any circuit, there are usually a number of design choices to be made. In this case, some of those include (in no particular order):

Feedback Path

Ideally, the feedback path would be as low-impedance as possible to maximize its immunity to capacitive coupling. For capacitors, impedance is inversely proportional to capacitance. I had a look through my parts bin and the lowest value capacitors I could find were 10 nF ceramic disc capacitors (marked 103).

Using 10 nF and the two different three-stage filters discussed earlier:

Amplifier

For the amplifier, I decided to go with an op-amp for the following reasons:

  1. I have more experience with op-amp circuits
  2. I have a lot of op-amps in my parts bin

I also have a box of assorted transistors, but since they are cheap generic parts from Amazon, they came with no documentation. This would make it much more difficult to debug potential issues as the characteristics of any given part are a mystery.

My choices of op-amps consisted of the parts I have on hand:

I decided it would be a good idea to break down the specifications of each to make a proper comparison. Here I only included the specs that I felt were most relevant to the application.

Specifications TL081CP TL082CP TL084CN UA741CN MC33079P
Supply Voltage ±5 V to ±15 V ±5 V to ±15 V ±5 V to ±15 V ±5 V to ±15 V ±5 V to ±18 V
Unity-Gain BW 3 MHz 3 MHz 3 MHz 1 MHz 9 MHz
29x Gain BW 103 kHz 103 kHz 103 kHz 34 kHz 310 kHz
Input Resistance ~ 1 TΩ ~ 1 TΩ ~ 1 TΩ 300 kΩ to 2 MΩ 175 kΩ
Output Resistance (not given) (not given) (not given) 75 Ω 37 Ω

Note: all of these parts I have are quite old, so the datasheets I got online may not be 100% accurate. For those curious, the date codes on these parts range from 1983 to 1995.

All of the above parts meet the power supply requirement, but the input impedance is a big difference. Because the feedback path is quite high-impedance by its nature, having a relatively low input impedance could dramatically affect the oscillation frequency. This means the UA741CN and MC33079P may not be suitable. The bandwidth of the UA741CN at the theoretical 29x gain is another issue, as having a bandwidth near the oscillation frequency could lead to unwanted attenuation in the amplification stage. Therefore, the TL08x family seemed like the best option given the parts available.

This page is a work-in-progress, further updates may be coming... eventually...

References

These are the references I found helpful in understanding the theory behind this circuit:

  1. Dungan, Frank R. (1992). Op Amps & Linear Integrated Circuits for Technicians, 2nd Edition.
  2. Mancini, Ron. (2000). Design of op amp sine wave oscillators. Texas Instruments. (link)

Tools Used

  1. Pen and paper
  2. Texas Instruments TI-84 Plus calculator
  3. Tektronix 2236 100 MHz analog oscilloscope
  4. GNU Octave (for graphing and double-checking math)
  5. LaTeX to Image Converter by Joseph Rautenbach (for writing the equations on this page)
  6. SIMetrix/SIMPLIS Elements (for schematic capture)